Macam-Macam Segitiga: Bentuk dan Sifatnya yang Menarik

Ilustrasi.(Freepik)

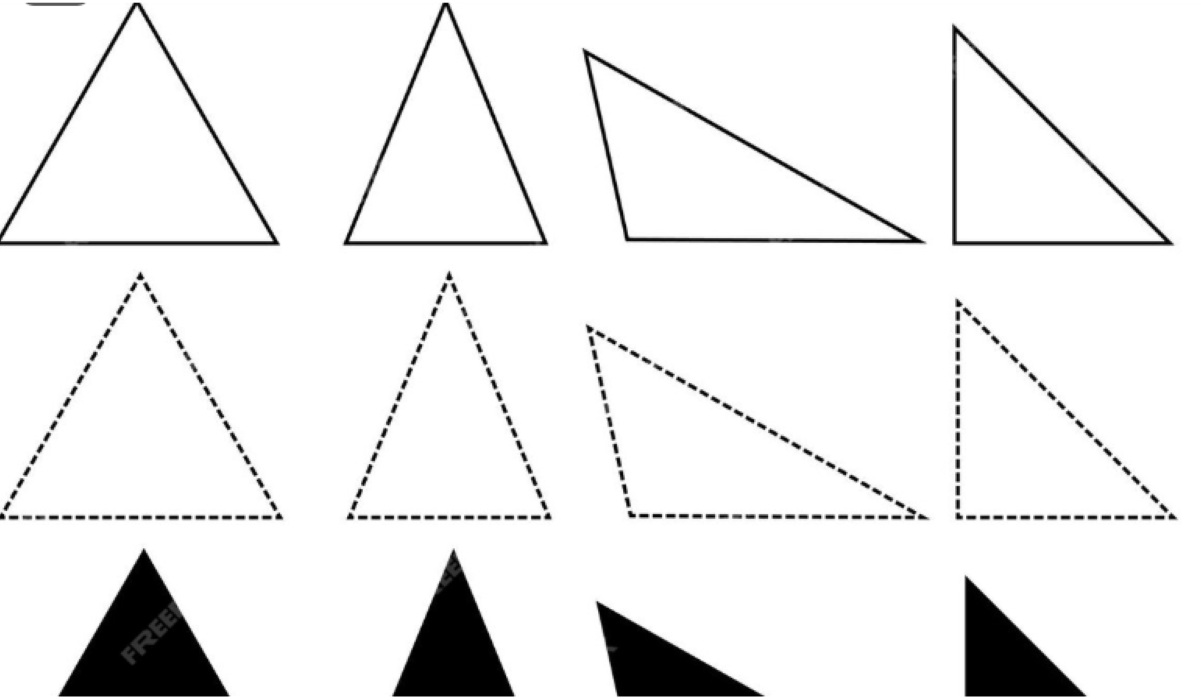
SEGITIGA, sebuah bangun datar fundamental dalam geometri, hadir dalam beragam wujud yang memikat. Keanekaragaman ini bukan sekadar variasi visual, melainkan juga perbedaan sifat-sifat yang mendasarinya. Memahami klasifikasi segitiga berdasarkan sisi dan sudut akan membuka wawasan lebih dalam tentang dunia geometri dan aplikasinya dalam kehidupan sehari-hari.

Klasifikasi Segitiga Berdasarkan Panjang Sisi

Pengelompokan segitiga berdasarkan panjang sisinya menghasilkan tiga kategori utama: segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Masing-masing memiliki karakteristik unik yang membedakannya.

Segitiga Sama Sisi: Kesempurnaan Simetri

Segitiga sama sisi adalah representasi visual dari kesempurnaan simetri. Ketiga sisinya memiliki panjang yang identik, menciptakan keseimbangan yang estetis. Konsekuensi dari kesamaan sisi ini adalah kesamaan ukuran ketiga sudutnya. Setiap sudut dalam segitiga sama sisi berukuran 60 derajat, menjadikannya segitiga yang juga sama sudut. Simetri yang melekat pada segitiga sama sisi membuatnya sering muncul dalam desain arsitektur, seni, dan bahkan alam, seperti pada bentuk kristal tertentu.

Segitiga Sama Kaki: Dua Sisi yang Serupa

Segitiga sama kaki menampilkan harmoni antara kesamaan dan perbedaan. Dua dari tiga sisinya memiliki panjang yang sama, sementara sisi ketiga, yang disebut alas, memiliki panjang yang berbeda. Sudut yang berhadapan dengan sisi yang sama panjang juga memiliki ukuran yang sama. Sifat ini memungkinkan segitiga sama kaki untuk memiliki sumbu simetri yang membagi alas menjadi dua bagian yang sama panjang dan tegak lurus terhadap alas. Contoh segitiga sama kaki dapat ditemukan pada layar perahu layar atau atap rumah tradisional.

Segitiga Sembarang: Keunikan Tanpa Kesamaan

Segitiga sembarang adalah bentuk yang paling umum dan beragam. Ketiga sisinya memiliki panjang yang berbeda, dan akibatnya, ketiga sudutnya juga memiliki ukuran yang berbeda. Tidak ada simetri yang melekat pada segitiga sembarang, menjadikannya bentuk yang fleksibel dan adaptif. Segitiga sembarang sering muncul dalam representasi topografi, desain grafis, dan berbagai aplikasi teknik.

Klasifikasi Segitiga Berdasarkan Ukuran Sudut

Selain panjang sisi, segitiga juga dapat diklasifikasikan berdasarkan ukuran sudut-sudutnya. Klasifikasi ini menghasilkan tiga kategori utama: segitiga lancip, segitiga siku-siku, dan segitiga tumpul.

Segitiga Lancip: Keindahan Sudut yang Tajam

Segitiga lancip adalah segitiga yang semua sudutnya berukuran kurang dari 90 derajat. Ketiga sudutnya lancip, menciptakan kesan visual yang ringan dan dinamis. Segitiga sama sisi selalu merupakan segitiga lancip, tetapi tidak semua segitiga lancip adalah segitiga sama sisi. Contoh segitiga lancip dapat ditemukan pada desain logo perusahaan atau elemen dekoratif.

Segitiga Siku-Siku: Kehadiran Sudut 90 Derajat

Segitiga siku-siku adalah segitiga yang memiliki satu sudut berukuran tepat 90 derajat. Sudut ini sering ditandai dengan simbol kotak kecil di sudut tersebut. Sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, dan merupakan sisi terpanjang dalam segitiga siku-siku. Dua sisi lainnya disebut kaki-kaki segitiga. Segitiga siku-siku memiliki peran penting dalam trigonometri dan teorema Pythagoras, yang menghubungkan panjang sisi-sisinya. Aplikasi segitiga siku-siku sangat luas, mulai dari konstruksi bangunan hingga navigasi.

Segitiga Tumpul: Keberadaan Sudut yang Lebar

Segitiga tumpul adalah segitiga yang memiliki satu sudut berukuran lebih dari 90 derajat. Sudut ini disebut sudut tumpul. Dua sudut lainnya harus lancip agar jumlah ketiga sudut tetap 180 derajat. Keberadaan sudut tumpul memberikan kesan visual yang terbuka dan luas. Contoh segitiga tumpul dapat ditemukan pada desain furnitur atau elemen arsitektur tertentu.

Hubungan Antara Klasifikasi Sisi dan Sudut

Penting untuk dicatat bahwa klasifikasi segitiga berdasarkan sisi dan sudut tidak saling eksklusif. Sebuah segitiga dapat termasuk dalam lebih dari satu kategori. Misalnya, segitiga sama sisi selalu merupakan segitiga lancip. Segitiga sama kaki dapat berupa segitiga lancip, siku-siku, atau tumpul, tergantung pada ukuran sudut-sudutnya. Segitiga sembarang juga dapat berupa segitiga lancip, siku-siku, atau tumpul. Pemahaman tentang hubungan ini memungkinkan kita untuk mengklasifikasikan segitiga secara lebih akurat dan komprehensif.

Sifat-Sifat Segitiga yang Fundamental

Selain klasifikasi berdasarkan sisi dan sudut, segitiga memiliki beberapa sifat fundamental yang berlaku untuk semua jenis segitiga:

Jumlah Sudut: Selalu 180 Derajat

Salah satu sifat segitiga yang paling mendasar adalah bahwa jumlah ketiga sudut dalamnya selalu 180 derajat. Sifat ini berlaku untuk semua jenis segitiga, tanpa memandang panjang sisi atau ukuran sudutnya. Sifat ini memungkinkan kita untuk menentukan ukuran sudut ketiga jika kita mengetahui ukuran dua sudut lainnya.

Ketidaksamaan Segitiga: Syarat Pembentukan Segitiga

Ketidaksamaan segitiga menyatakan bahwa jumlah panjang dua sisi segitiga harus selalu lebih besar dari panjang sisi ketiga. Sifat ini merupakan syarat penting agar tiga garis dapat membentuk sebuah segitiga. Jika ketidaksamaan ini tidak terpenuhi, maka ketiga garis tersebut tidak akan dapat membentuk sebuah segitiga.

Luas Segitiga: Ukuran Permukaan

Luas segitiga adalah ukuran permukaan yang dibatasi oleh ketiga sisinya. Rumus umum untuk menghitung luas segitiga adalah 1/2 alas tinggi, di mana alas adalah panjang salah satu sisi segitiga dan tinggi adalah jarak tegak lurus dari alas ke sudut yang berhadapan. Terdapat juga rumus lain untuk menghitung luas segitiga, seperti rumus Heron, yang menggunakan panjang ketiga sisi.

Keliling Segitiga: Panjang Total Sisi

Keliling segitiga adalah jumlah panjang ketiga sisinya. Keliling merupakan ukuran panjang total garis yang membentuk segitiga. Menghitung keliling segitiga relatif sederhana, hanya dengan menjumlahkan panjang ketiga sisinya.

Aplikasi Segitiga dalam Kehidupan Sehari-hari

Segitiga bukan hanya konsep abstrak dalam geometri, tetapi juga memiliki aplikasi yang luas dalam kehidupan sehari-hari. Bentuk segitiga dapat ditemukan dalam berbagai bidang, mulai dari arsitektur hingga teknik, seni, dan bahkan alam.

Arsitektur dan Konstruksi: Kekuatan dan Stabilitas

Segitiga sering digunakan dalam arsitektur dan konstruksi karena kekuatannya dan stabilitasnya. Bentuk segitiga mampu mendistribusikan beban secara merata, sehingga struktur yang menggunakan segitiga menjadi lebih kuat dan tahan terhadap tekanan. Contoh penggunaan segitiga dalam arsitektur adalah pada rangka atap, jembatan, dan menara.

Teknik: Presisi dan Akurasi

Dalam bidang teknik, segitiga digunakan untuk berbagai keperluan, seperti pengukuran, pemetaan, dan desain. Prinsip-prinsip trigonometri, yang didasarkan pada segitiga siku-siku, digunakan untuk menghitung jarak, sudut, dan ketinggian dengan presisi dan akurasi. Segitiga juga digunakan dalam desain pesawat terbang, kapal, dan kendaraan lainnya untuk meningkatkan aerodinamika dan efisiensi.

Seni dan Desain: Estetika dan Harmoni

Segitiga sering digunakan dalam seni dan desain untuk menciptakan komposisi yang menarik dan harmonis. Bentuk segitiga dapat memberikan kesan dinamis, stabil, atau seimbang, tergantung pada orientasi dan proporsinya. Segitiga juga digunakan dalam desain logo, poster, dan elemen dekoratif lainnya.

Alam: Keindahan dan Efisiensi

Bentuk segitiga dapat ditemukan di alam dalam berbagai wujud, seperti pada bentuk kristal, sarang lebah, dan sayap serangga. Bentuk segitiga seringkali merupakan solusi yang paling efisien dan optimal untuk berbagai masalah struktural dan fungsional. Misalnya, sarang lebah menggunakan bentuk heksagonal, yang terdiri dari segitiga-segitiga sama sisi, untuk memaksimalkan ruang penyimpanan dan meminimalkan penggunaan bahan.

Teorema Pythagoras: Hubungan Sisi pada Segitiga Siku-Siku

Teorema Pythagoras adalah salah satu teorema paling terkenal dan fundamental dalam matematika, khususnya dalam geometri. Teorema ini hanya berlaku untuk segitiga siku-siku dan menyatakan bahwa kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi lainnya (kaki-kaki segitiga). Secara matematis, teorema Pythagoras dapat ditulis sebagai: a² + b² = c², di mana a dan b adalah panjang kaki-kaki segitiga, dan c adalah panjang hipotenusa.

Teorema Pythagoras memiliki aplikasi yang sangat luas dalam berbagai bidang, seperti konstruksi, navigasi, dan fisika. Dalam konstruksi, teorema ini digunakan untuk memastikan bahwa sudut-sudut bangunan adalah siku-siku. Dalam navigasi, teorema ini digunakan untuk menghitung jarak antara dua titik. Dalam fisika, teorema ini digunakan untuk menghitung resultan vektor.

Trigonometri: Hubungan Sudut dan Sisi pada Segitiga

Trigonometri adalah cabang matematika yang mempel...